APLICACIÓN DE LAS CONICAS EN LA ARQUITECTURA

Se llama Cónicas a todas las curvas intersección entre un cono y un plano; si dicho plano no pasa por el vértice, se obtienen las cónicas propiamente dichas. Se clasifican en cuatro tipos: elipse, parábola, hipérbola y circunferencia.

A las cónicas las podemos observa todos los días al salir a pasear, caminar, en auto o a cualquier lugar donde vayamos, son tan importantes dentro de la Arquitectura ya que se presentan hasta en los detalles mínimos de un espacio decorado; por ejemplo en las puertas, ventanas, columnas, algunas paredes, pasamanos, etc.

Dónde aplico las cónicas en la arquitectura?

Todas ellas tienen una gran importancia en la Arquitectura, ya que la misma forma tiene una buena resistencia estructural, y estética se utilizan con mayor frecuencia arcos con forma elíptica.

Este uso se ve dado en puentes, anfiteatros, en escaleras, cúpulas, estadios, etc

Las construcciones modernas también nos permiten observar el uso de las cónicas, estando presentes en los puentes, en el ámbito estructural, peso; también presentes en cúpulas en el variando de la estructura y función; también en escaleras y balcones y en diferentes partes de una edificación, se podrá apreciar las cónicas.

Circunferencia

La circunferencia es el conjunto de todos los puntos de un plano que están a una distancia fija de un centro. El uso de la circunferencia en la arquitectura es excelente ya que permite el ahorro en superficies de muros y cerramientos, ya que se la considera como la forma más eficiente de todas. Una obra reconocida a nivel mundial por su belleza y gran tamaña es: El ojo de Londres.

La circunferencia es comúnmente utilizada en redondeles, estadios, cúpulas.

Parábola

La parábola es un lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado foco, y de una recta llamada directriz. Para la arquitectura tiene una gran importancia, ya que su forma tiene una gran resistencia para las construcciones ya sea de manera estética o estructural.

A ésta se la encuentra en reconocidas obras arquitectónicas las cuales nos prueban que son aptas para grandes obras entre estas tenemos: Oceanografic, Gateway Arch, Puente de ventas.

Elipse

La elipse es el lugar geométrico de los puntos del plano tales que la suma de las distancias a dos puntos fijos llamados focos es constante. En la arquitectura se le ha encontrado una gran utilidad ya que se la encuentra en anfiteatros y estadios.

Entre los más reconocidos están: Stade de France, The Cybertecture Egg, Anfiteatro de Capua.

Hipérbola

Es un lugar geométrico de los puntos del plano tales que la diferencia de sus distancias a dos puntos fijos llamados focos siempre es constante y menor que la distancia entre los focos.

Oscar Niemeyer realizo una de sus más grandes obras como es la Catedral de Brasilia la cual basándose en el uso de las hipérbolas. Ésta tiene una pureza desde cualquier punto que se la observe, ya que presenta una gran religiosidad. Otras obras que también son reconocidas por su forma son: la Torre de Koba, torre de control del Aeropuerto de Barcelona, Puente hiperbólico de Manchester.

Aplicación de las Matrices en la Arquitectura

La matriz es una representación gráfica que permite descubrir cualquier tipo de relación deseada entre actividades, por medio de ejes cartesianos que se prolongan y forman una retícula, sobre la cual se vacían los datos deducidos

Existen tres tipos de matrices:

Matriz de espacios

Matriz por zonas

Matriz por áreas

Tipos de matrices en la Arquitectura

Matriz de relaciones

La matriz Es una representación gráfica que permite descubrir cualquier tipo de relación deseada entre actividades, por medio de ejes cartesianos que se prolongan y forman una retícula, sobre la cual se vacían los datos deducidos.

Para realizar la matriz es necesario establecer los tipos de relación, partiendo de algunos criterios:

-Relación Necesaria: Es la relación indispensable entre dos o más espacios, implica una dependencia total de un espacio con otro.

-Relación Deseable: La dependencia no es total y la proximidad de los espacios es solamente “deseable” o conveniente, los espacios funcionan sin necesidad de la presencia del otro.

-Relación Inexistente: Cuando no existe ningún tipo de relación entre los espacios.

BIBLIOGRAFIA:

http://arquitecturafauunfv.blogspot.com/

http://mateunfv.blogspot.com/

http://www.espe.edu.ec/portal/files/libros/analisis/capi10p.pdf

www.google.com

FUNCIONES

Función es una relación entre un conjunto dado X (el dominio) y otro conjunto de elementos Y (el recorrido) de forma que a cada elemento del dominio le corresponde un único elemento del recorrido.

Una función es una regla de correspondencia entre dos conjuntos de tal manera que a cada elemento del primer conjunto le corresponde uno y sólo un elemento del segundo conjunto.

EJEMPLO:

Identificar dominio y rango de la función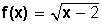

Como la función tiene radicales el dominio está conformado por todos los valores para los cuales x – 2 ≥ 0.

Esto es, el dominio de la función incluye todos los reales que son mayores o iguales a 2.

El rango es igual al conjunto de los números reales positivos incluyendo el cero; puesto que al reemplazar los valores del dominio se obtienen únicamente valores positivos bajo la función f.

FUNCIONES TRIGONOMÉTRICAS

En matemáticas, las funciones trigonométricas son las funciones establecidas con el fin de extender la definición de las razones trigonométricas a todos los números reales y complejos.

Las funciones trigonométricas son de gran importancia en física, astronomía, cartografía, náutica, telecomunicaciones, la representación de fenómenos periódicos, y otras muchas aplicaciones.

Cómo usar la trigonometría en la arquitectura

La matemática hace el diseño de edificios más seguro y más preciso. La trigonometría es especialmente importante en la arquitectura, ya que permite al arquitecto calcular las distancias y las fuerzas relacionadas con elementos de la diagonal. De las seis funciones de trigonometría básicas, el seno, el coseno y la tangente son los más importantes para la arquitectura, ya que permiten al arquitecto encontrar fácilmente los valores opuestos y adyacentes relacionados con un ángulo o la hipotenusa, la traducción de un vector diagonal en vectores horizontales y verticales.

FUNCION EXPONENCIAL

La función exponencial es del tipo:

Sea a un número real positivo. La función que a cada número real x le hace corresponder la potencia a^x se llama función exponencial de base a y exponente x.

Ejemplos

x	y = 2^x
-3	1/8
-2	1/4
-1	1/2
0	1
1	2
2	4
3	8

Propiedades de la función exponencial

Dominio: .

Recorrido: R +

Es continua.

Los puntos (0, 1) y (1, a) pertenecen a la gráfica.

Es inyectiva toda

a ≠ 1(ninguna imagen tiene más de un original).

Creciente si a > 1.

Decreciente si a < 1.

Las curvas y = a^x e y = (1/a)^x son simétricas respecto del eje OY.

Funcion exponencial en la arquitectura

Las funciones exponenciales se aplican en la arquitectura para planificar el desarrollo urbano de una ciudad en la que notablemente ha crecido la población, esto ayudará a la regeneración urbana y construcción de urbanizaciones con las instalaciones que cubran las necesidades de toda la población de dicho territorio.

FUNCION LOGARITMO

Una función logarítmica es aquella que genéricamente se expresa como f (x) == log_ax, siendo a la base de esta función, que ha de ser positiva y distinta de 1.

La función logarítmica en base a es la función inversa de la exponencial en base a.

Ejemplo:

x
1/8	-3
1/4	-2
1/2	-1
1	0
2	1
4	2
8	3

Propiedades de la función logarítmica

Las propiedades generales de la función logarítmica se deducen a partir de las de su inversa, la función exponencial. Así, se tiene que:

La función logarítmica sólo existe para valores de x positivos, sin incluir el cero. Por tanto, su dominio es el intervalo (0,+¥).
Las imágenes obtenidas de la aplicación de una función logarítmica corresponden a cualquier elemento del conjunto de los números reales, luego el recorrido de esta función es R.
En el punto x = 1, la función logarítmica se anula, ya que log_a 1 = 0, en cualquier base.
La función logarítmica de la base es siempre igual a 1.
Finalmente, la función logarítmica es continua, y es creciente para a > 1 y decreciente para a < 1.

Funcion Logaritmo en la arquitectura

La arquitectura igualmente debe aplicar en este tipo de funcion los cálculos y diseños debe aplicarse con la exactitud que el caso amerita y se debe prolijamente aplicar las matemáticas.
En arquitectura emplea la funcion de logaritmo cuando queremos determinar la altura de un edificio usando la base y el ángulo.

FUNCION ALGEBRAICA

Las funciones algebraicas son aquellas cuya regla de correspondencia es una expresión algebraica, siendo a la vez una función que satisface una ecuación polinómica cuyos coeficientes son a su vez polinomios.

En matemáticas, una función algebraica es una función que satisface una ecuación polinómica cuyos coeficientes son a su vez polinomios o monomios. Por ejemplo, una función algebraica de una variable x es una solución y a la ecuación

donde los coeficientes ai(x) son funciones polinómicas de x. Una función que no es algebraica es denominada una función trascendente.

Funcion Algebraica en la arquitectura

El arquitecto usa las funciones algebraicas, dado un ejemplo, cuando hace negocios con países vecinos que usan otra moneda; el precio en pesos (por ejemplo) está dado en función del precio del dólar. Explicación: si queremos comprar en pesos algo que cuesta 100 dólares... necesitamos aplicar una función, si el dólar cuesta 14 pesos el producto costaría 1400 pesos pero si el dólar está en 10 pesos, el producto costara 1000, Un valor depende de otro eso es una función.

BIBLIOGRAFIA:

http://www.profesorenlinea.cl/matematica/Funciones_matematicas.html
http://es.wikipedia.org/wiki/Funci%C3%B3n_trigonom%C3%A9trica
http://www.ehowenespanol.com/trigonometria-arquitectura-como_127481/
http://matematicascercanas.com/2014/04/06/la-piramide-de-keops/
http://www.vitutor.com/fun/2/c_13.html
http://www.hiru.com/matematicas/funcion-logaritmica
http://matematica.laguia2000.com/general/funcion-algebraica
www.google.com

LIMITES Y CONTINUIDAD DE UNA FUNCION

LIMITES

El límite de una función es un concepto fundamental del análisis matemático, un caso de límite aplicado a las funciones.

Informalmente, el hecho que una función f tiene un límite L en el punto c, significa que el valor de f puede ser tan cercano a L como se desee, tomando puntos suficientemente cercanos a c, independientemente de lo que ocurra en c.

Propiedades de los Limites

Si f(x) y g(x) son funciones de variable real y k es un escalar, entonces, se cumplen las siguientes propiedades:

Límite de	Expresión
Una constante	$\lim_{x \to c} k =\, k,\, donde\, k\in \R \,$
La función identidad	$\lim_{x \to c} x = \, c \,$
El producto de una función y una constante	$\lim_{x \to c} kf(x) =\, k\lim_{x \to c} f(x)\,$
Una suma	$\lim_{x \to c} (f(x) + g(x)) =\, \lim_{x \to c} f(x) + \lim_{x \to c} g(x)\,$
Una resta	$\lim_{x \to c} (f(x) - g(x)) =\, \lim_{x \to c} f(x) - \lim_{x \to c} g(x)\,$
Un producto	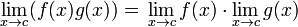$\lim_{x \to c} (f(x) g(x)) =\, \lim_{x \to c} f(x) \cdot \lim_{x \to c} g(x)\,$
Un cociente	$\lim_{x \to c} {{f(x)}\over {g(x)}} =\, {{\lim_{x \to c} {f(x)}} \over {\lim_{x \to c} {g(x)}}}\,\ \mbox{si } \lim_{x \to c} g(x) \ne 0,$
Una potencia	${\lim_{x \to c} f(x)^{g(x)}} =\, {\lim_{x \to c} f(x)^{\lim_{x \to c} g(x)}}\,\ \mbox{si } f(x) > 0$
Un logaritmo	${\lim_{x \to c} \log f(x)} =\, \log {\lim_{x \to c} f(x)}$
El número e	${\lim_{x \to 0} \left(1+x\right)^{1 \over x}} =\, {\lim_{x \to \infty} \left(1+{1 \over x}\right)^x } =\, e$
Función f(x) acotada y g(x) infinitesimal	${\lim_{x \to c} \left(f(x) \cdot g(x)\right)} =\, 0$ .

LIMITES UNILATERALES

LIMITES UNILATERALES POR LA DERECHA:

Sea f una función definida en todos los números del intervalo abierto (a, c). Entonces, el límite de f (x), cuando x se aproxima a a por la derecha es L, y se escribe

LIMITES UNILATERALES POR LA IZQUIERDA:

Sea f una función definida en todos los números de (d, a). Entonces, el límite de f (x), cuando x se aproxima a por la izquierda es L, y se escribe

LIMITES INFINITOS

El infinito es una idea muy especial. Sabemos que no podemos alcanzarlo, pero podemos calcular el valor de funciones que tienen al infinito dentro.

Una función f(x) tiene por límite +∞ cuando x → a, si fijado un número real positivo K > 0 se verifica que f(x) > k para todos los valores próximos a a.

Ejemplo

APLICACIONES EN LA ARQUITECTURA

Los arquitectos utilizan los límites de una función para saber el crecimiento de una colonia en la cual se va a trabajar; y el trabajo que éste desempeñará, al construir una vivienda más por cada habitante que se integre.

Además se la ocupa si se va a construir una obra en la que debes realizar aproximaciones con un margen de error mínimo debes usar límites.

CONTINUIDAD DE FUNCIONES

CONTINUIDAD EN UN PUNTO

El término continuo aplicado a una función de variable real sugiere que su gráfica no debe presentar saltos; es decir, que al trazar su gráfica no se requiera alzar la mano. Sin embargo se hace necesario formalizar matemáticamente esta definición.

El termino continuo a una función de variable real sugiere que su gráfica no debe presentar saltos, es decir que al trazar su grafica no se requiera alzar la mano. Sin embargo se hace necesario formalizarlo matematicamente esta definición.

Se dice que una función f(x) es continua en un punto a, si y sólo, si se verifican las condiciones siguientes:

· La función existe en a.

· Existe límite de f(x) cuando x tiende a a.

· El valor de la función en el punto y el límite en dicho punto son iguales:

Cuando no se cumple alguna de las anteriores condiciones, se dice que la función es discontinua en el punto.

Por otra parte, se considera que la función es continua en un intervalo (a, b) cuando es continua en todo punto x, tal que a < x < b.

Como ejemplos de funciones discontinuas en un punto.

Ejercicios de continuidad

CONTINUIDAD EN UN INTERVALO

La representación gráfica de esta función es la siguiente:

También se tiene que una función (f) definida en el intervalo (a, b), es continua en ese intervalo, si y solo si es continúa en el intervalo abierto (a, b) y es continua por la derecha de "a".

1.- Continuidad en un Intervalo ABIERTO

EJEMPLO:

2.- Continuidad en un Intervalo CERRADO

Ejemplo:

APLICACIONES en la ARQUITECTURA:

En la arquitectura se utiliza en la continuidad de un intervalo en las:

-Deformaciones de vigas

-Diseño de estructuras de puentes

-Momentos de estructuras de vigas columnas, losas

BIBLIOGRAFIA:
-http://es.wikipedia.org/wiki/L%C3%ADmite_de_una_funci%C3%B3n
- http://es.wikipedia.org/wiki/L%C3%ADmite_matem%C3%A1tico
- http://www.vitutor.com/fun/3/a_3.html
- http://matematica.50webs.com/limite-infinito.html
- http://www.vitutor.com/fun/3/b_1.html
-https://www.dspace.espol.edu.ec/bitstream/123456789/781/2/1486.pdf
- http://www.vadenumeros.es/primero/ejercicios-de-continuidad.htm

APLICACIONES DE LAS DERIVADAS

Concepto:

La función derivada de una función f(x) es una función que asocia a cada número real su derivada, si existe. Se expresa por f'(x).

En matemáticas, la derivada de una función es una medida de la rapidez con la que cambia el valor de dicha función matemática, según cambie el valor de su variable independiente. La derivada de una función es un concepto local, es decir, se calcula como el límite de la rapidez de cambio media de la función en un cierto intervalo, cuando el intervalo considerado para la variable independiente se torna cada vez más pequeño. Por ello se habla del valor de la derivada de una cierta función en un punto dado.

La derivada de la función en el punto marcado equivale a la pendiente de la recta tangente (la gráfica de la función está dibujada en rojo; la tangente a la curva está dibujada en verde).

EJEMPLO:

Determinar la función derivada de f(x) = x² − x + 1.

REGLAS BÁSICAS DE DERIVACIÓN

1ª) LA DERIVADA DE UNA CONSTANTE POR UNA FUNCIÓN es igual a la constante por la derivada de la función:

2ªa) LA DERIVADA DE UNA SUMA DE FUNCIONES es igual a la suma de las derivadas de las funciones:

2ªb) LA DERIVADA DE UNA DIFERENCIA DE FUNCIONES es igual a la diferencia de las derivadas de las funciones:

3ª) LA DERIVADA DE UN PRODUCTO DE FUNCIONES es igual a la derivada de la primera función por la segunda función sin derivar más la primera función sin derivar por la derivada de la segunda función:

4ª) LA DERIVADA DE UN COCIENTE DE FUNCIONES es igual a la derivada de la función del numerador por la función del denominador sin derivar, menos la función del numerador sin derivar por la derivada de la función del denominador, dividido todo ello por la función del denominador al cuadrado:

5ª) LA DERIVADA DE UNA FUNCIÓN ELEVADA A OTRA es igual a la derivada de la expresión como exponencial más la derivada de la expresión como potencial:

DERIVADAS APLICADAS A LA ARQUITECTURA

Las derivadas están siempre presentes. Se utiliza en arquitectura. En el campo de las construcciones, los arquitectos, ingenieros y profesionales de estas áreas usualmente emplean las derivadas para determinar el límite en superficies irregulares; áreas y volúmenes de regiones y sólidos de revolución es decir de cilindros, conos, etc. Concretamente, el que trata de asuntos vinculados con la derivada se denomina cálculo diferencial.

Además las derivaciones se las utiliza para hallar máximos, mínimos, concavidad, convexidad, inflexiones de alguna figura geométrica.

Superficie paraboloide

LOS MANATIALES

La forma que caracteriza esta construcción es la de una superficie conocida como paraboloide hiperbólico o "silla de montar"

Tipo de arquitectura.

Se lo utiliza en todo tipo de arquitectura; tradicional y moderna.

REGLA DE LA CADENA

En cálculo, la regla de la cadena es una fórmula para la derivada de la composición de dos funciones. Tiene aplicaciones en el cálculo algebraico de derivadas cuando existe composición de funciones.

FORMULA:

[u(x)^m]' = m · u(x)^{m - 1} · u'(x)

EJERCICIO

Calcular la derivada de f(x) = (x²+ 1)³.

RESOLUCIÓN:

· Si u = x²+ 1,

u' = 2x

En este caso m = 3

· f'(x) = 3 (x² + 1)² · 2x = 6x (x² + 1)²

Máximos y mínimos

Máximos

Si f y f' son derivables en a, a es un máximo relativo o local si se cumple:

1. f'(a) = 0

2. f''(a) < 0

Mínimos

Si f y f' son derivables en a, a es un mínimo relativo o local si se cumple:

1. f'(a) = 0

2. f''(a) > 0

http://www.vadenumeros.es/imagenes/primero/derivadas-maximos.gif

EJEMPLO:

f(x) = x³ − 3x + 2

1. Hallamos la derivada primera y calculamos sus raíces.

f'(x) = 3x² − 3 = 0

x = −1 x = 1.

2. Realizamos la 2ª derivada, y calculamos el signo que toman en ella los ceros de derivada primera y si:

f''(x) > 0 Tenemos un mínimo.

f''(x) < 0 Tenemos un máximo.

f''(x) = 6x

f''(−1) = −6 Máximo

f'' (1) = 6 Mínimo

3. Calculamos la imagen (en la función) de los extremos relativos.

f(−1) = (−1)³ − 3(−1) + 2 = 4

f(1) = (1)³ − 3(1) + 2 = 0

Máximo(−1, 4) Mínimo(1, 0)

BIBLIOGRAFIA:

http://www.derivadas.es/

http://www.dervor.com/derivadas/derivadas_funciones.html

http://www.monografias.com/trabajos62/derivada-funciones/derivada-funciones.shtml

http://optimaticosum.blogspot.com/2013_08_01_archive.html

http://www.sectormatematica.cl/contenidos/cadena.htm}

http://www.dervor.com/derivadas/maximos_mimimos.html

APLICACIÓN DE INTEGRALES EN LA ARQUITECTURA

La aplicación de las integrales en la arquitectura es muy variada, su principal objetivo es crear diseños en edificaciones con formas complejas y dinámicas.

Función primitiva

Función primitiva de una función dada f(x), es otra función F(x) cuya derivada es la función dada.

F'(x) = f(x)

Integral indefinida

Integral indefinida es el conjunto de las infinitas primitivas que puede tener una función.

Se representa por ∫ f(x) dx.

Se lee : integral de x diferencial de x.

∫ es el signo de integración.

f(x) es el integrando o función a integrar.

dx es diferencial de x, e indica cuál es la variable de la función que se integra.

C es la constante de integración y puede tomar cualquier valor numérico real.

Si F(x) es una primitiva de f(x) se tiene que:

∫ f(x) dx = F(x) + C

Para comprobar que la primitiva de una función es correcta basta con derivar.

EJEMPLO:

APLICACIONES A LA ARQUITECTURA

En lo que a arquitectura en general, esta clase de calculo de lo utiliza para crear proyectos con formas complejas y dinámicas.

Y se las aplica en las siguientes tipos de arquitectura:

http://wiki.ead.pucv.cl/images/6/61/Stuttgart-21regi.jpg

PROYECTO ESTACION DE TRENES STUTTGART 21

MUSEO OSCAR NIEMEYER

BIBLIOGRAFIA:

http://wiki.ead.pucv.cl/index.php/Estadio_Olimpico_de_Munich_/Fried_Otto_-_Sagrada_Familia_/A.Gaudi_-_Proyecto_Stuttgart_21

http://www.vitutor.com/integrales/indefinidas/integral_indefinida.html

http://www.inetor.com/indefinidas/formulas_integrales.html

http://es.slideshare.net/franklingualaquiza/aplicacin-de-la-integral-definida-en-la-arquitectura

http://www.inetor.com/indefinidas/definicion_integral.html

http://www.vitutor.com/integrales/indefinidas/integral_indefinida.html

ARQUITECTURA

sábado, 22 de noviembre de 2014

Matematicas Aplicadas en ARQUITECTURA

Matriz de relaciones

Cómo usar la trigonometría en la arquitectura

Ejemplos

Propiedades de la función exponencial

Dominio: .

Funcion exponencial en la arquitectura

Propiedades de la función logarítmica

Funcion Logaritmo en la arquitectura

Funcion Algebraica en la arquitectura

LIMITES Y CONTINUIDAD DE UNA FUNCION

Propiedades de los Limites

CONTINUIDAD DE FUNCIONES

CONTINUIDAD EN UN PUNTO

Ejercicios de continuidad

APLICACIONES DE LAS DERIVADAS

Concepto:

La función derivada de una función f(x) es una función que asocia a cada número real su derivada, si existe. Se expresa por f'(x).

Máximos y mínimos

APLICACIÓN DE INTEGRALES EN LA ARQUITECTURA

Función primitiva

Integral indefinida

4 comentarios:

Archivo del blog